EXCEL: Buscar valor entre dos números

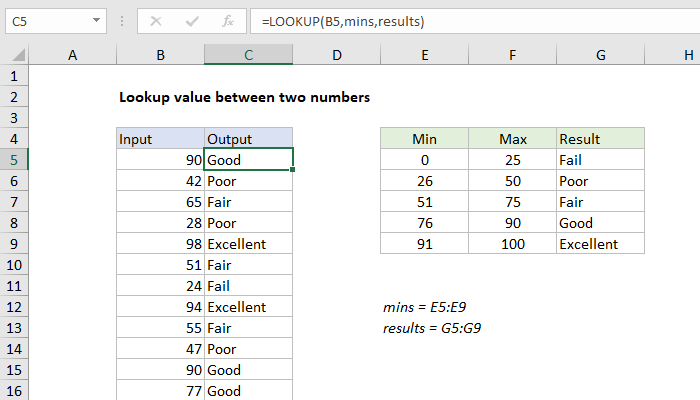
Para buscar valores entre dos valores y devolver un resultado correspondiente, puede usar la función BUSCAR y una tabla ordenada. En el ejemplo que se muestra, la fórmula en C5 es:

=BUSCAR(B5,mins,results)

donde "minutos" es el rango nombrado E5: E9, y "resultados" es el rango nombrado G5: G9.

Cómo funciona esta fórmula

La función BUSCAR realiza una búsqueda de coincidencias aproximada en un rango y devuelve el valor correspondiente en otro.

Aunque la tabla en este ejemplo incluye valores máximos y mínimos, solo necesitamos usar los valores mínimos. Esto se debe a que cuando BUSCAR no puede encontrar una coincidencia, coincidirá con el siguiente valor más pequeño. BUSCAR se configura así:

• The lookup values come from column B.
• The lookup vector is entered as the named range "mins" (E5:E9)
• The result vector is entered as the named range "results" (G5:G9)

BUSCAR se comporta así:

• If LOOKUP encounters an exact match in the lookup vector, the corresponding value in the result vector is returned.
• If no exact match is found, LOOKUP will traverse the lookup vector until a larger value is found, then "step back" to the previous row and return a result.
• If the lookup value is greater than the largest value in the lookup vector, LOOKUP will return a result associated with the last value in the lookup vector.

Nota: los valores en el vector de búsqueda deben ordenarse en orden ascendente.

Literalmente entre

Aunque el ejemplo anterior funciona bien y efectivamente ubica un valor "entre" un mínimo y máximo en la tabla de búsqueda, en realidad solo usa los valores mínimos. Con un rango con nombre "maxs" para valores máximos, puede escribir una versión literal de la fórmula como esta:

=BUSCAR(2,1/((B5>=mins)*(B5<=maxs)),results)

Esta versión devuelve el valor asociado en el vector de resultados cuando el valor en B5 está literalmente entre el valor mínimo y el máximo en una fila dada. En caso de duplicados, esta fórmula devolverá la última coincidencia. La explicación de la lógica está aquí.